Multi-Objective Optimization (MOO)
Many real-world applications involve multi-objective optimization problems, such as developing models that are both accurate and fair, designing agents that are powerful yet energy-efficient, and discovering drug formulations that meet multiple criteria. However, these objectives often conflict with each other, making it impossible to optimize all of them simultaneously with a single solution.
Multi-Objective Optimization Problem
We consider the following multi-objective optimization problem (MOP) with \(m\) objective functions \(\boldsymbol{f} = \{f_1,\cdots, f_m\}: \mathcal{X} \rightarrow \mathbb{R}^m\) in the decision space \(\mathcal{X} \subseteq \mathbb{R}^n\):
\[\min_{x \in \mathcal{X}} \ \boldsymbol{f}(x) = (f_1(x),f_2(x),\cdots, f_m(x)).\]For a non-trivial problem, the objective functions \(\{f_1,\cdots, f_m\}\) will conflict with each other, hence cannot be simultaneously optimized by a single best solution. For multi-objective optimization, we have the following definition on dominance relation among solutions:
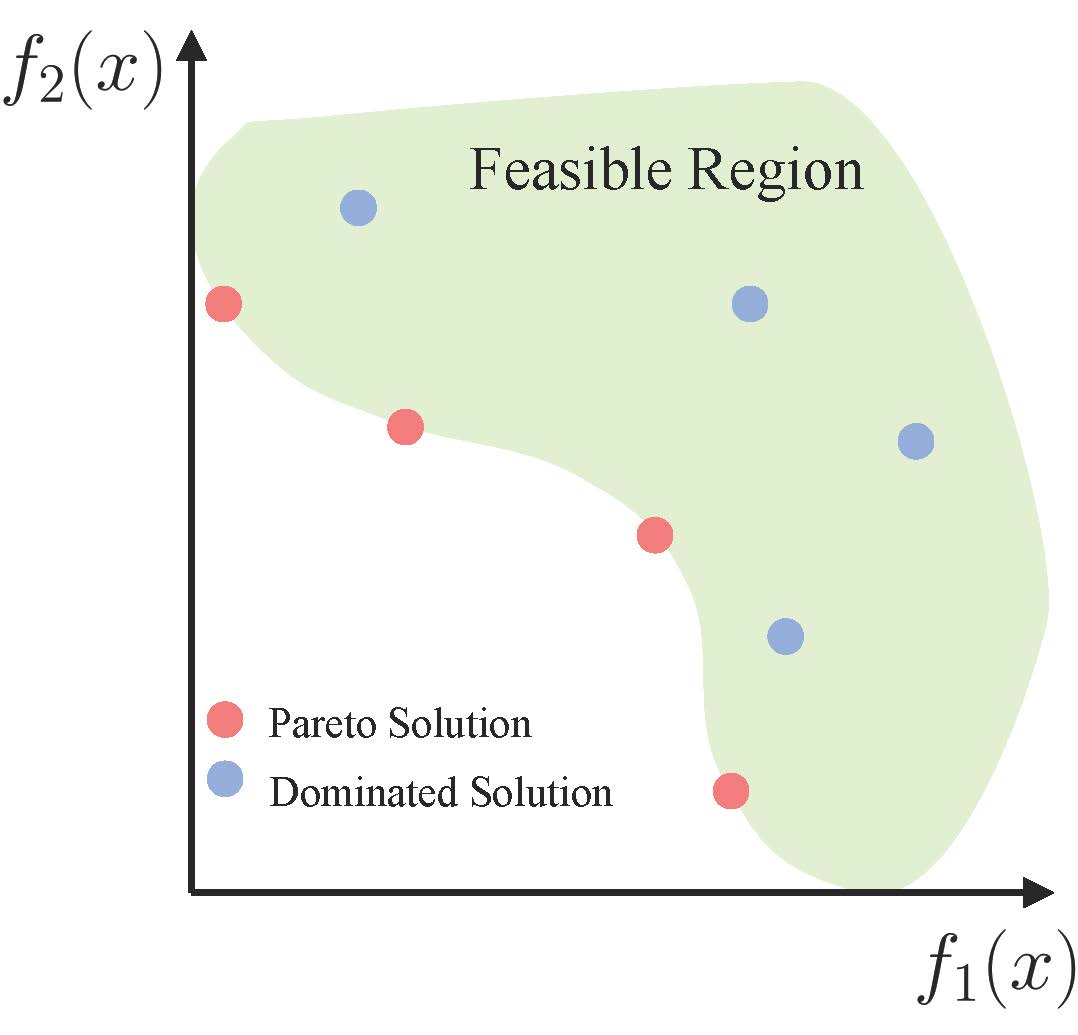
Definition 1 (Dominance): Let \(x^{(a)},x^{(b)} \in \mathcal{X}\) be two solutions for a multi-objective optimization problem, \(x^{(a)}\) is said to dominate \(x^{(b)}\), denoted as \(\boldsymbol{f}(x^{(a)}) \prec \boldsymbol{f}(x^{(b)})\), if and only if \(f_i(x^{(a)}) \leq f_i(x^{(b)}) \ \forall i \in \{1,...,m\}\) and \(f_j(x^{(a)}) < f_j(x^{(b)}) \ \exists j \in \{1,...,m\}\).
The dominance relation only establishes a partial order among different solutions since any two solutions may be non-dominated with each other (e.g., \(\boldsymbol{f}(x^{(a)}) \nprec \boldsymbol{f}(x^{(b)})\) and \(\boldsymbol{f}(x^{(b)}) \nprec \boldsymbol{f}(x^{(a)})\)). In this case, the solution \(x^{(a)}\) and \(x^{(b)}\) are said to be incomparable. Therefore, we have the following definition of Pareto optimality to describe the optimal solutions for multi-objective optimization:
Definition 2 (Pareto Optimality): A solution \(x^{\ast} \in \mathcal{X}\) is Pareto optimal if there is no \(x \in \mathcal{X}\) such that \(\boldsymbol{f}(x) \prec \boldsymbol{f}(x^{\ast})\).
Similarly, a solution \(x^*\) is called local Pareto optimal if it is Pareto optimal in \(\mathcal{X} \cap B(x^*,\delta)\), of which \(B(x^*,\delta) = \{x \in \mathbb{R}^n \mid \|x - x^*\| < \delta \}\) is an open ball around \(x^*\) with radius \(\delta > 0\). In general, the Pareto optimal solution is not unique, and the set of all Pareto optimal solutions is called the Pareto set:
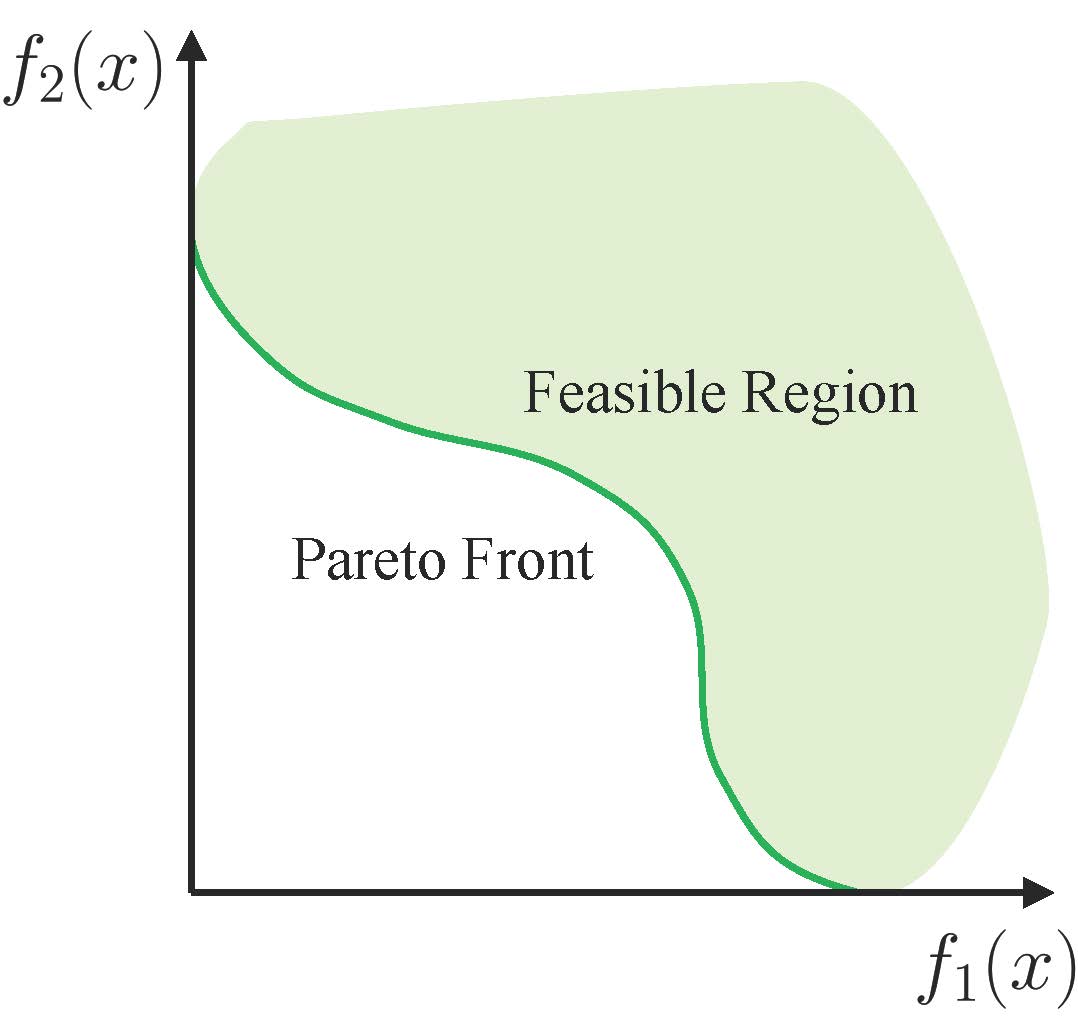
\[X^* = \{x \in \mathcal{X} \mid f(\hat x) \nprec f(x) \ \forall \hat x \in \mathcal{X} \}.\]Its image in the objective space is called the Pareto front:
\[f(X^*) = \{f(x) \in \mathbb{R}^m \mid x \in X^* \}.\]Under mild conditions, the Pareto set \(X^*\) and the Pareto front \(\boldsymbol{f}(X^*)\) are both \((m-1)\)-dimensional manifolds in the decision space \(\mathbb{R}^n\) and objective space \(\mathbb{R}^m\), respectively.
Representative Work from Optima Group
MOEA/D
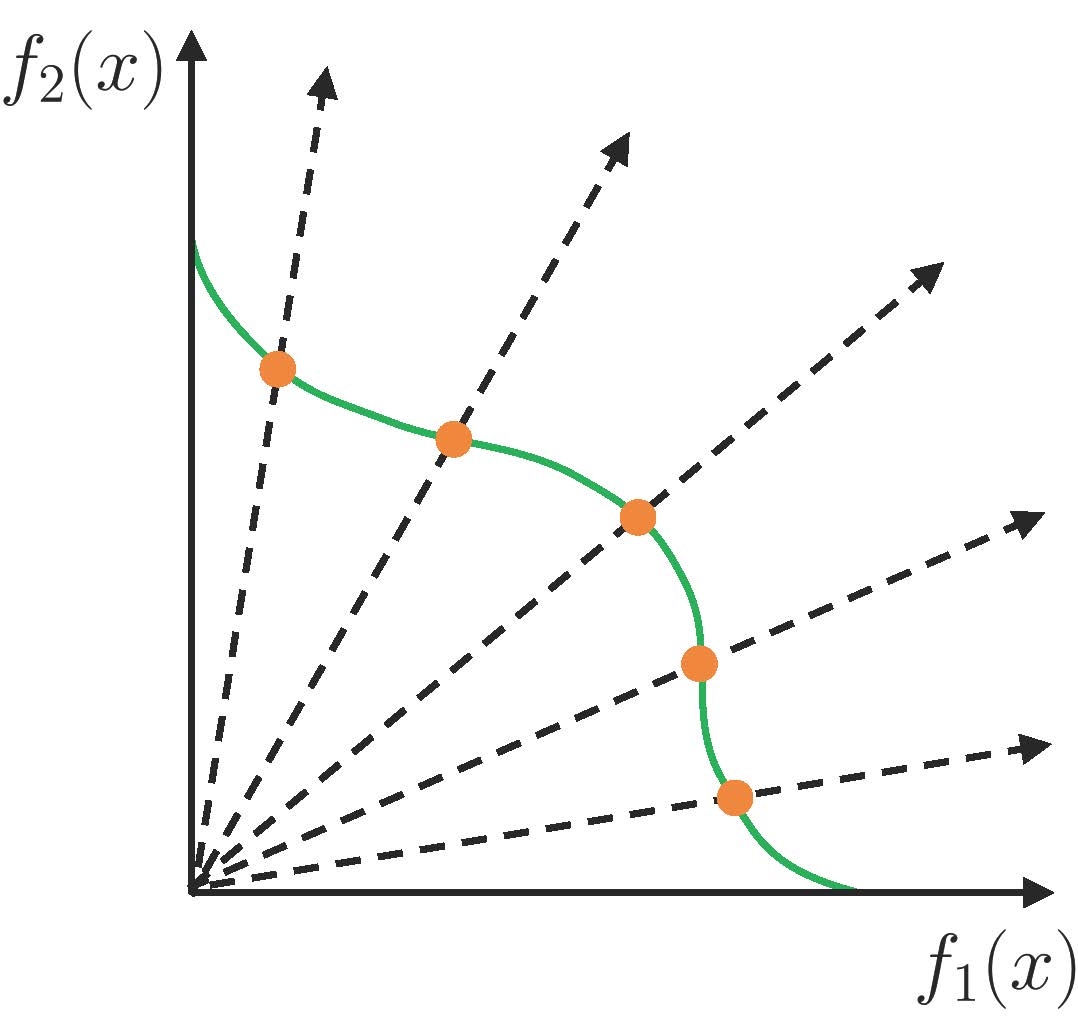
The decomposition-based multiobjective evolutionary algorithms (MOEA/D) [1], proposed by Prof. Qingfu Zhang, is one of the three most widely used evolutionary multiobjective optimization (EMO) methodologies. It decomposes a multi-objective problem into a number of single-objective subproblems and optimizes them simultaneously using collaborative information among neighboring subproblems. This strategy allows MOEA/D to efficiently produce a diverse set of Pareto solutions with different optimal trade-offs.
MOEA/D has successfully built a natural bridge between traditional multiobjective optimization and EMO which were separated improperly before, and provides a vehicle for making the best use of well-developed single objective optimization optimizer in EMO. The MOEA/D paper has been cited over 9800 times according to Google Scholar, and is the most cited paper among all the papers published on IEEE Transactions on Evolutionary Computation (TEVC) since 2003.
Efficient Gradient-based Multi-Objective Optimization
In recent years, the Optima research group has developed numerous efficient gradient-based methods for finding a set of diverse Pareto solutions and applied these methods to address various real-world application problems, particularly in multi-objective machine learning. In [2], we proposed Pareto Multi-Task Learning (Pareto MTL), a novel approach that decomposes multi-task learning problems into a set of constrained subproblems, each representing a specific trade-off preference. By solving these subproblems in parallel, Pareto MTL identifies a well-representative set of Pareto optimal solutions. In [3], we introduced the Smooth Tchebycheff Scalarization (STCH), a theoretically sound method that ensures exact Pareto solutions for any valid trade-off with fast convergence and low per-iteration complexity. In addition, we have proposed methods to align Pareto solutions with user-specific preferences [4], generate uniformly distributed solutions on the Pareto front [5], and explore their applications in adversarial attacks for deep neural networks [6, 7].
Pareto Set Learning for Multi-Objective Optimization
 |
 |
| Classic Multi-Objective Optimization | Pareto Set Learning |
|---|
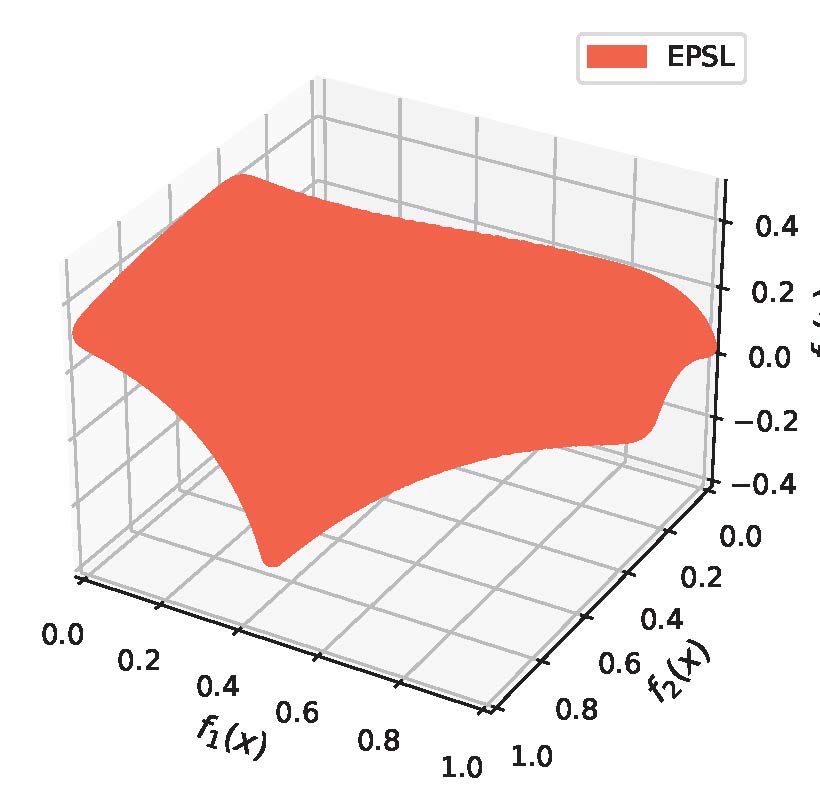
The Pareto set is typically a manifold that contains an infinite number of optimal solutions, each representing a unique trade-off among the objectives. The existing methods, however, can only identify a single or finite subset of these solutions. This limitation is significant because a finite set of solutions cannot fully capture the structure of the whole Pareto set, and there is a high likelihood that the decision-maker’s most preferred solution(s) may not be included in the found solution set. We proposed a novel Pareto set learning method that learns the entire Pareto set using a single model [8]. This approach enables decision-makers to explore the entire approximate Pareto set in real time, accommodating any valid trade-off preference, which is a capability critical for many real-world applications. We have successfully applied this method to multi-task learning [8], combinatorial optimization [9], and expensive optimization problems [10]. Furthermore, we have advanced this work by analyzing its theoretical properties [11], extending it to handle structure constraints on the solution set [12, 13], and generalizing it to single-objective homotopy optimization [14].
Few for Many: Finding a Small Set of Solutions for Many-Objective Optimization
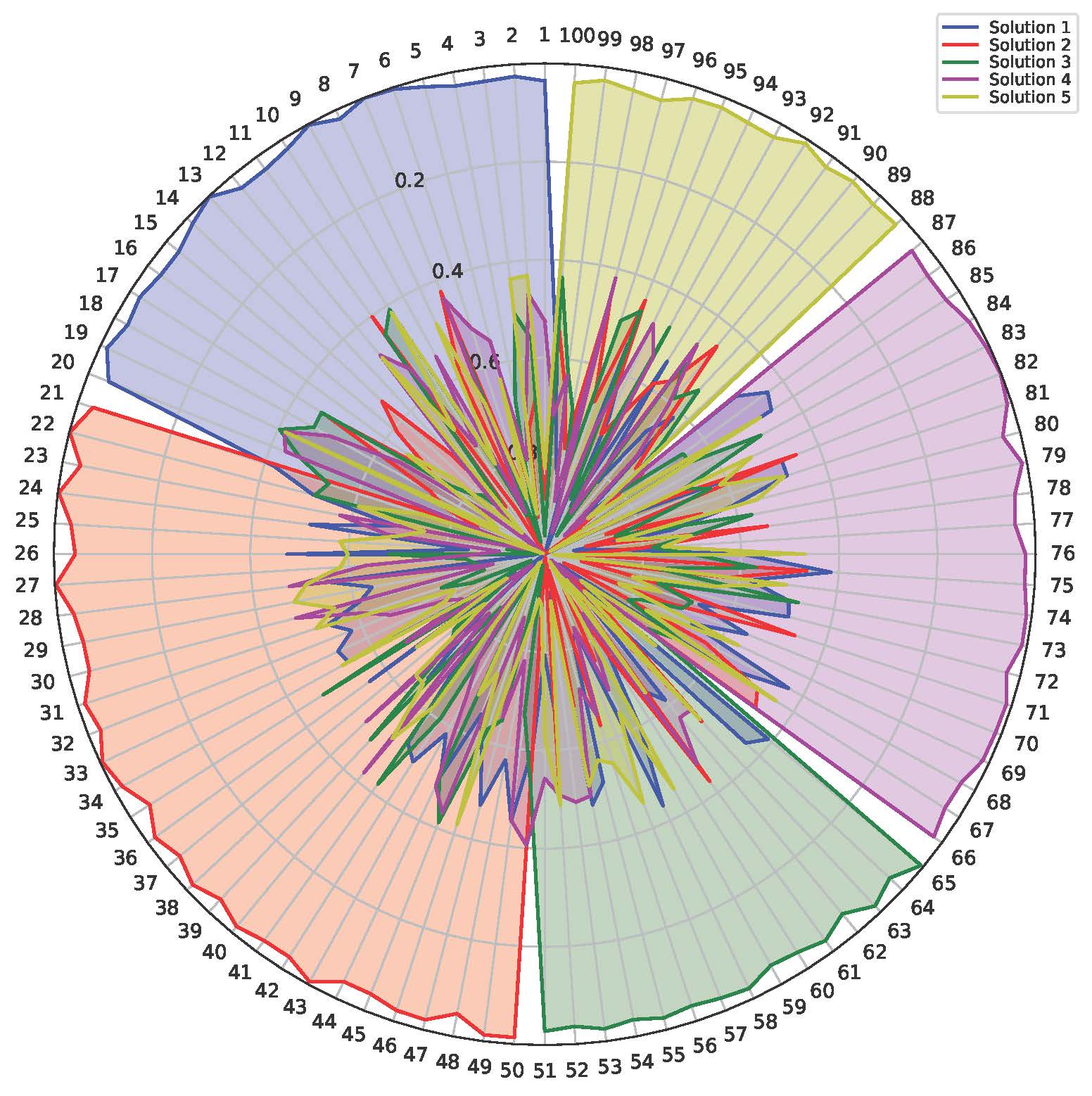
The required number of solutions to well approximate the whole Pareto set could be exponentially large with respect to the number of objectives, which makes the classic methods unsuitable for handling a large number of optimization objectives. In our recent work [15], we propose a novel and principled few-for-many approach to find a small set of solutions (e.g., \(5\)) to handle a large number of optimization objectives (e.g., \(100\)) in a collaborative and complementary manner. In this way, each optimization objective should be well addressed by at least one solution in the small solution set. This setting is important for many applications, such as constructing a small portfolio of algorithms to handle many optimization problems, producing a few different versions of advertisements to serve a large group of diverse audiences, and building a small set of machine learning models to handle many different data or tasks (e.g., mixture of experts). However, this demand is currently underexplored in the multi-objective optimization community. We hope our work can attract attention from both researchers and practitioners, and lead to many exciting follow-up work in this research direction.
Survey and Software
To facilitate further research and applications, we have also released the LibMOON software package [17] and wrote a survey paper [18] on gradient-based multi-objective optimization and its applications in deep learning.
References
[1] Qingfu Zhang, Hui Li. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6):712–731, 2007.
[2] Xi Lin, Hui-Ling Zhen, Zhenhua Li, Qingfu Zhang, Sam Kwong. Pareto Multi-Task Learning, NeurIPS 2019.
[3] Xi Lin, Xiaoyuan Zhang, Zhiyuan Yang, Fei Liu, Zhenkun Wang, Qingfu Zhang. Smooth Tchebycheff Scalarization for Multi-Objective Optimization, ICML 2024.
[4] Xiaoyuan Zhang, Xi Lin, Qingfu Zhang. PMGDA: A Preference-based Multiple Gradient Descent Algorithm. IEEE Transactions on Emerging Topics in Computational Intelligence 2024.
[5] Xiaoyuan Zhang, Genghui Li, Xi Lin, Yichi Zhang, Yifan Chen, Qingfu Zhang. Gliding over the Pareto Front with Uniform Designs, NeurIPS 2024.
[6] Ping Guo, Cheng Gong, Xi Lin, Zhiyuan Yang, Qingfu Zhang. Exploring the Adversarial Frontier: Quantifying Robustness via Adversarial Hypervolume. EEE Transactions on Emerging Topics in Computational Intelligence 2024.
[7] Ping Guo, Cheng Gong, Fei Liu, Xi Lin, Zhichao Lu, Qingfu Zhang, Zhenkun Wang. MOS-Attack: A Scalable Multi-objective Adversarial Attack Framework. Technical Reports 2025.
[8] Xi Lin, Zhiyuan Yang, Qingfu Zhang, Sam Kwong. Controllable Pareto Multi-Task Learning. Technical Reports 2020.
[9] Xi Lin, Zhiyuan Yang, Qingfu Zhang. Pareto Set Learning for Neural Multi-Objective Combinatorial Optimization, ICLR 2022.
[10] Xi Lin, Zhiyuan Yang, Xiaoyuan Zhang, Qingfu Zhang. Pareto Set Learning for Expensive Multi-Objective Optimization, NeurIPS 2022.
[11] Xiaoyuan Zhang, Xi Lin, Bo Xue, Yifan Chen, Qingfu Zhang. ypervolume Maximization: A Geometric View of Pareto Set Learning, NeurIPS 2023.
[12] Ping Guo, Qingfu Zhang, Xi Lin. Approximation of a Pareto Set Segment Using a Linear Model with Sharing Variables, EMO 2023.
[13] Xi Lin, Xiaoyuan Zhang, Zhiyuan Yang, Qingfu Zhang. Dealing with Structure Constraints in Evolutionary Pareto Set Learning, IEEE Transactions on Evolutionary Computation 2025.
[14] Xi Lin, Zhiyuan Yang, Xiaoyuan Zhang, Qingfu Zhang. Continuation Path Learning for Homotopy Optimization, ICML 2023.
[15] Xi Lin, Yilu Liu, Xiaoyuan Zhang, Fei Liu, Zhenkun Wang, Qingfu Zhang. Few for Many: Set Tchebycheff Scalarization for Multi-Objective Optimization, ICLR 2025.
[16] Yilu Liu, Chengyu Lu, Xi Lin, Qingfu Zhang. Many-Objective Cover Problem: Discovering Few Solutions to Cover Many Objectives, PPSN 2024.
[17] Xiaoyuan Zhang, Liang Zhao, Yingying Yu, Xi Lin, Zhenkun Wang, Han Zhao, Qingfu Zhang. LibMOON: A Gradient-based MultiObjective OptimizatioN Library in PyTorch, NeurIPS 2024.
[18] Weiyu Chen, Xiaoyuan Zhang, Baijiong Lin, Xi Lin, Han Zhao, Qingfu Zhang, James T. Kwok. Gradient-Based Multi-Objective Deep Learning: Algorithms, Theories, Applications, and Beyond, Technical Reports 2025.