Evolutionary Computation

Evolutionary Computation (EC) is a family of optimization algorithms gleaned from biological evolution. These algorithms emulate natural processes such as mutation, recombination, and selection to iteratively evolve a population of solutions. Key members of this family include genetic algorithm, genetic programming, and evolution strategy. Over the years, EC has been successfully applied to a variety of domains, including engineering optimization, autonomous agents, and machine learning.

Evolution Strategy and Black-box Optimization

Evolution Strategy (ES) stands out as one of the most powerful approaches for optimizing black-box function [1]. ES distinguishes itself from most other EC algorithms by featuring self-adaptive mutation operators, which aligns with the principled natural gradient ascent. Recent years have witness a growing interest in ES due to their versatility in different domains, including reinforcement learning, adversarial attack [2], and parametric optimization [3,4].

In general, an ES formulates a black-box optimization problem using a distribution model:

\[\operatorname{maximize}_{x\in\mathcal{X}}f(x)\Rightarrow\operatorname{maximize}_{\theta\in\Theta}\mathcal{J}(\theta)=\mathbb{E}_{x\sim \mathcal{N}_{\theta}}[f(x)],\]

where \(f\) exposes no information other than its function value, and \(\mathcal{N}_{\theta}\), as in most cases, is a (multivariate) Gaussian distribution, and \(\theta\) its parameters. With the formulation, the natural gradient \(\tilde{\nabla}\mathcal{J}(\theta)\) can be estimated. In this sense, the reproduction of new solutions in EC amounts to the Monte-Carlo estimate of \(\tilde{\nabla}\mathcal{J}(\theta)\). Most modern ESs define \(\theta=(m,\sigma,C)\), where \(m\in\mathbb{R}^n\) is the distribution mean, \(\sigma>0\) is called the step-size or mutation strength, and \(C\in\mathbb{S}_{++}^{n}\) is the covariance matrix.

Covariance Matrix Adaptation Evolution Strategy (CMA-ES) has remained a state-of-the-art (SOTA) variant of modern ESs. Besides its foundation in natural gradient ascent, two key components, the cumulative step-length adaptation and the rank-one update based on the evolution path, attribute to its success.

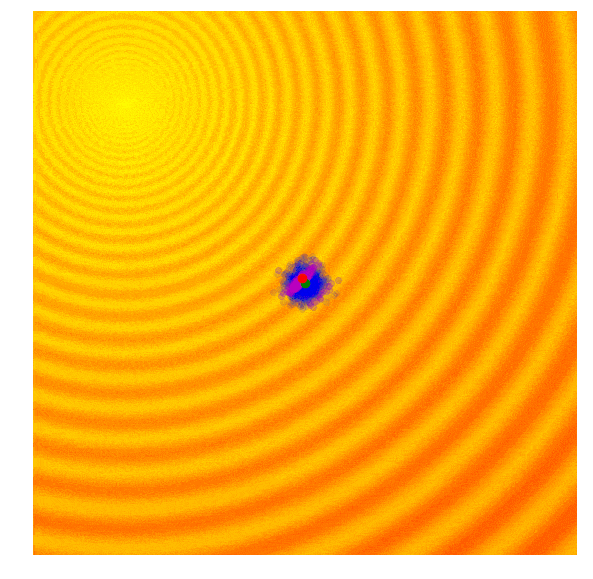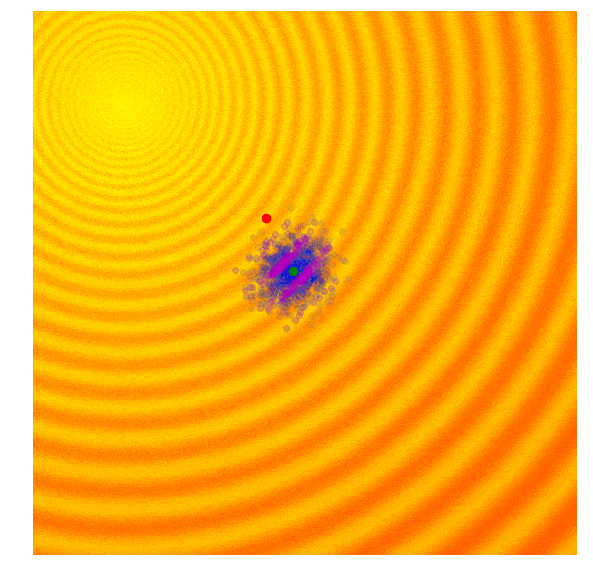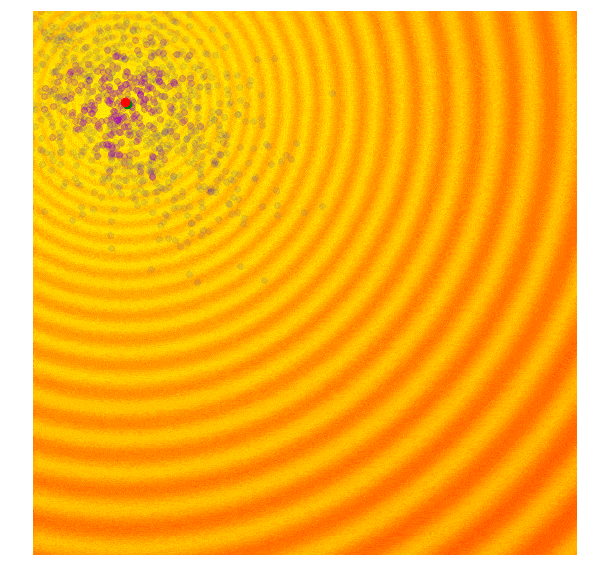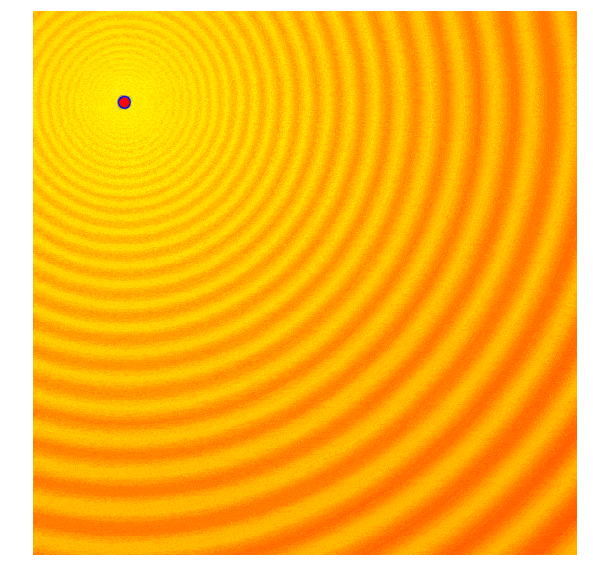
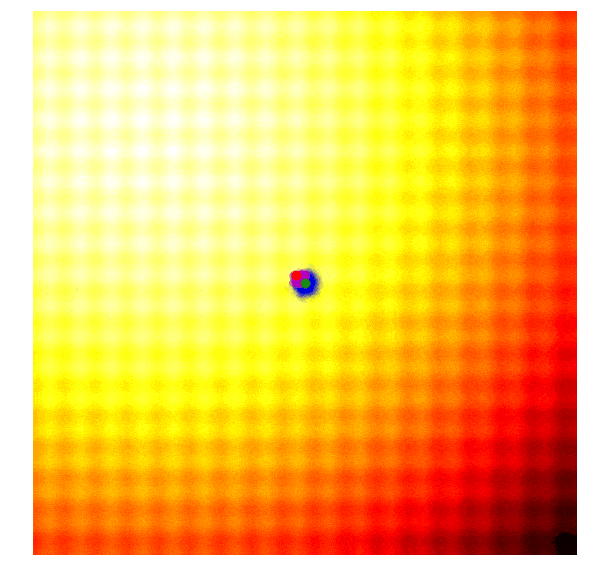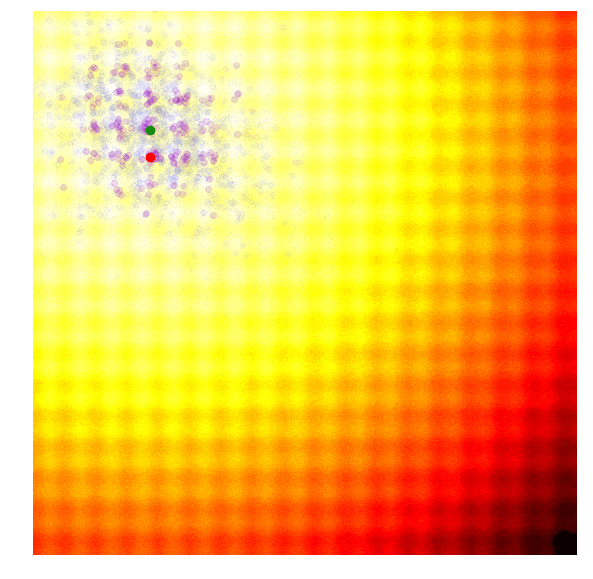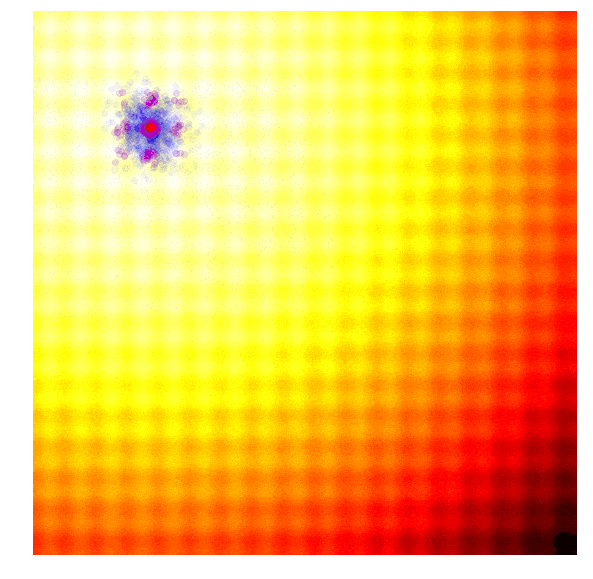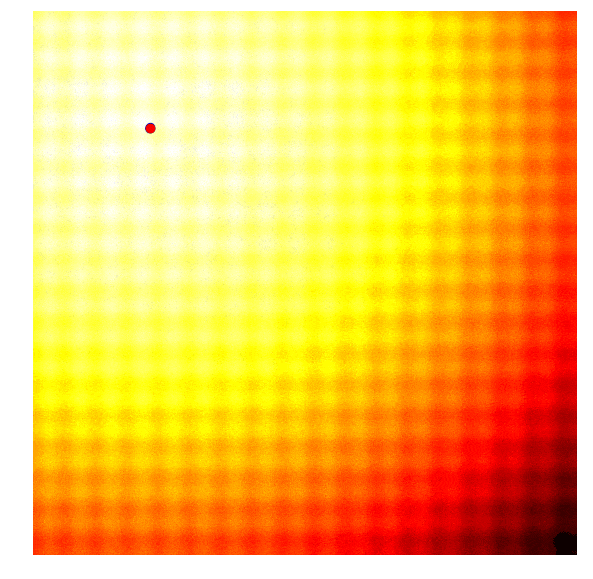
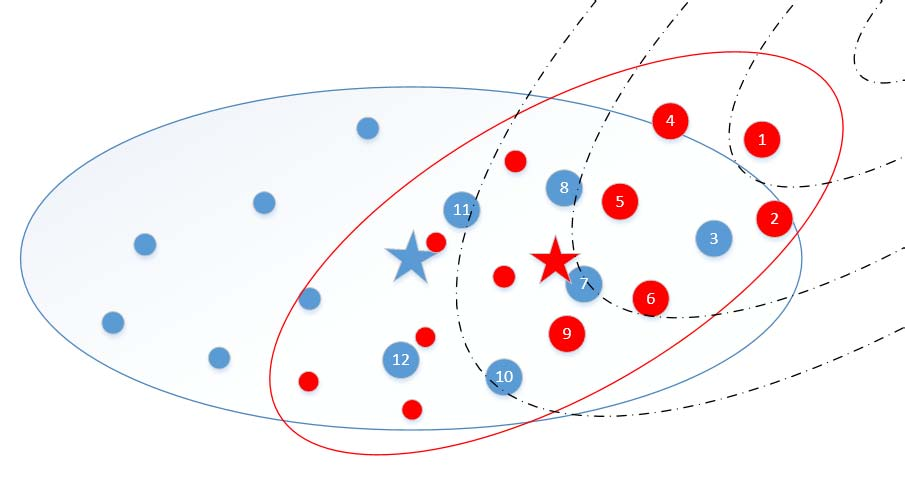
The search process by CMA-ES on two toy problems (Image source: David Ha’s blog).

Representative Work From the Optima Group

Applying ESs to large-scale (e.g., \(n\geq 1000\)) black-box optimization problems centers on the recent development of ESs. A non-elitist CMA-ES suffers from \(\mathcal{O}(n^2)\) time & space complexity, data hungriness, and a slow learning rate proportional to \(1/n^2\) for the covariance matrix [1]. The Optima research group has developed several advanced ES algorithms to address these issues [5-9].

In [5], we propose Rm-ES, which achieves \(\mathcal{O}(n)\) time complexity and has been shown effective on large-scale problems. It utilizes a low-rank model as the covariance matrix, which is expressed as:

\[C=\alpha I+\sum_{i=1}^{m}\beta_ip_ip_i^T\]

where \(\alpha>0\) and \(\beta_i>0\) are hyper-parameters, \(I\) is the identity matrix, and \(p_i\) is the evolution path. We illustrate that the evolution path accumulates natural gradients of the expected fitness with respect to the distribution mean, and acts as a momentum term under the stationarity condition. Experiments on the BBOB and CEC’2010 LSGO benchmarks demonstrated that Rm-ES outperformed CMA-ES as well as other SOTA large-scale variants. Since its publication, Rm-ES has been officially compared with several SOTA ES variants on the standard large-scale BBOB benchmark and included in popular libraries such as PyPop7.

Recently, we have been dedicated to leveraging the strength of ESs in multiobjective optimization, especially MOEA/D, to tackle difficult multiobjective problems, e.g., when non-separability and ill-conditioning are involved [10].

References

[1] Zhenhua Li, Qingfu Zhang. Evolution strategies for continuous optimization: A survey of the state-of-the-art. Swarm and Evolutionary Computation 56 (2020): 100694.

[2] Zhenhua Li, Huilin Cheng, Xinye Cai, Jun Zhao, Qingfu Zhang. SA-ES: Subspace activation evolution strategy for black-box adversarial attacks. IEEE Transactions on Emerging Topics in Computational Intelligence 7.3 (2022): 780-790.

[3] Xi Lin, Zhiyuan Yang, Xiaoyuan Zhang, Qingfu Zhang. Continuation path learning for homotopy optimization. International Conference on Machine Learning. PMLR, 2023.

[4] Xi Lin, Xiaoyuan Zhang, Zhiyuan Yang, Qingfu Zhang. Dealing With Structure Constraints in Evolutionary Pareto Set Learning. IEEE Transactions on Evolutionary Computation (2025).

[5] Zhenhua Li, Qingfu Zhang. A simple yet efficient evolution strategy for large-scale black-box optimization. IEEE Transactions on Evolutionary Computation 22.5 (2017): 637-646.

[7] Zhenhua Li, Qingfu Zhang, Xi Lin, Hui-Ling Zhen. Fast covariance matrix adaptation for large-scale black-box optimization. IEEE transactions on cybernetics 50.5 (2018): 2073-2083.

[8] Zhenhua Li, Jingda Deng, Weifeng Gao, Qingfu Zhang, Hai-Lin Liu. An efficient elitist covariance matrix adaptation for continuous local search in high dimension. 2019 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2019.

[9] Zhenhua, Li, Qingfu Zhang. An efficient rank-1 update for Cholesky CMA-ES using auxiliary evolution path. 2017 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2017.

[10] Chengyu Lu, Yilu Liu, and Qingfu Zhang. MOEA/D-CMA Made Better with (l+ l)-CMA-ES. 2024 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2024.